728x90
SMALL
- 이전 글에서 데이터 분석이 우연을 수학적으로 계산하고, 그 속의 규칙성을 찾아내는 과정이라고 언급한 적이 있습니다.
- 이런 규칙적이고 확률적인 패턴을 구조적으로 잘 설명해주는 것이 바로 확률 분포입니다.
확률 분포는 뭔가요?
- 확률 분포는 확률 변수가 가질 수 있는 값들과 그 값이 나타날 확률의 구조를 표현한 것입니다.
- 말이 조금 어렵게 들릴 수 있지만, 단순하게 말하면 "이 데이터는 이런 값들이 이런 비율로 나온다"를 알려주는 지도로 보면 됩니다.
- 이 확률 분포는 크게 2가지로 나뉩니다.
이산확률분포와 연속확률분포
- 이산확률분포는 셀 수 있는 값에 대한 분포로, 대표적으로 이항분포, 초기하분포, 포아송분포 등이 있습니다. 그리고 확률질량함수(PMF)로 표현됩니다.
- 연속확률분포는 값이 연속적(무한히 많음)일 때 쓰이는 분포로, 대표적으로 정규분포, t 분포, 카이제곱, F 분포, 지수분포 등이 있습니다. 이 분포는 확률밀도함수(PDF)로 표현됩니다.
- 이 중에서 t 분포는 모집단의 분산을 모르는 상황에서 표본 평균을 추정하거나 가설 검정을 할 때 매우 유용합니다.
- 이처럼 모집단의 분포를 알 수 없는 제한된 상황에서 분포를 통해 통계적 추론을 할 수가 있게 됩니다 !!!
이산확률분포에 또 다른 분포도 있나요?
- 대표적인 4가지 분포에 대해서만 말씀드리겠습니다.
- 먼저 균등분포가 있습니다. X가 동일한 확률을 가지는 분포를 균등분포라고 합니다.
- 그리고 이항분포가 있습니다. 이름에서도 알 수 있듯, 1과 0의 값만을 가지는 분포입니다. 주식 가격이 앞으로 3일간 매일 오를 확률을 구할 때 적용될 수도 있습니다.
- 여기서 베르누이 시행이라는 말이 나오는데, 베르누이 시행은 이항분포를 나타낼 수 있는, 결과가 두 가지 중 하나만 나오는 시행을 뜻합니다.
- 베르누이 시행은 각각의 결과가 독립적으로 이루어지기 때문에 처음에 0이 나왔다고 해서 다음에 나올 값에 영향을 받지 않고,
- 각각의 시행은 상호독립적이고, p(성공 확률)는 매 시행마다 동일하고, n(전체 시행 횟수)은 사전에 정해져 있습니다.
- 초기하분포도 있는데, 이항 분포와 달리 각 시행이 서로 독립적이지 않아서 시행마다 성공 확률이 달라집니다.
- 왜냐하면 이항 분포는 복원추출이지만, 초기하분포는 비복원 추출이기 때문입니다.
- 마지막으로 포아송분포가 있습니다. 일정한 관측 공간에서 특정 사건이 발생하는 횟수를 나타내는 분포입니다.
- 포아송분포는 품질 관리나 보험상품 개발 등에 주로 사용되는 분포입니다.
- 예시로, 특정 연령대에서 평균 몇 번의 교통사고가 발생하는지 계산하여 보험료를 산정할 때 포아송 분포가 활용됩니다.
- 그렇게 해야 기업 입장에서 손해를 보지 않으면서, 고객을 유인할 수 있는 합리적인 보험 상품을 개발할 수 있을 것입니다.
- 발생하는 사건은 양의 정수 형태를 가지고, 모든 사건은 독립적으로 발생하며, 해당 시공간에서 사건의 발생 비율은 항상 같습니다.
- 그리고 한 번에 둘 이상의 사건이 발생하지 않습니다.
그럼 연속확률분포에는 어떤 게 있나요?
- 여기서는 기본적인 정규분포와 지수분포에 대해서만 언급하겠습니다!
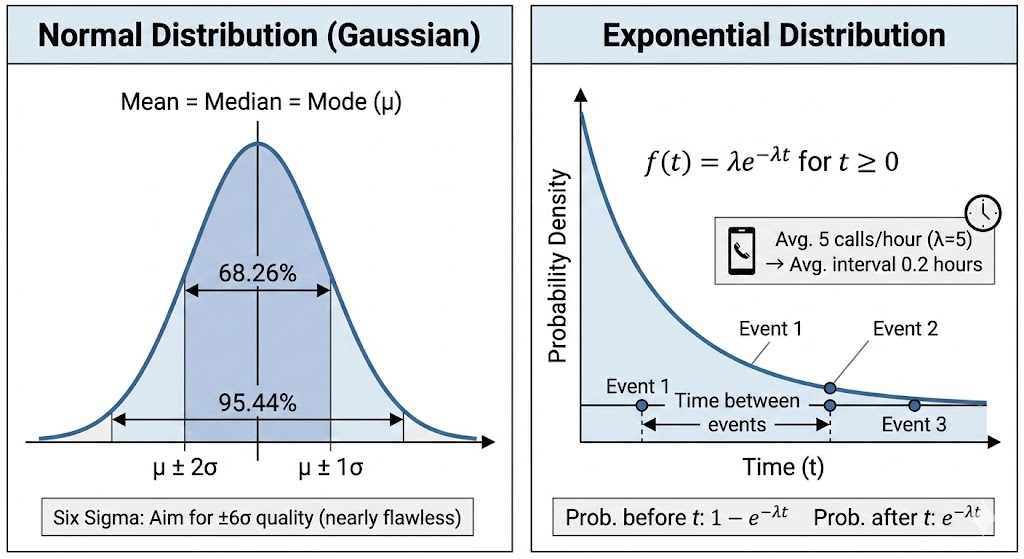
정규 분포
- 가우스가 물리 실험에서 발생하는 오차의 확률 분포가 정규 곡선과 같다는 것을 증명해 정규분포를 가우스 분포(Gaussian distribution)라고 부르기도 합니다.
- 정규 분포가 성립되기 위해서는 몇 가지 조건을 만족해야 합니다.
- 평균 중심 좌우 대칭의 종 모양의 형태를 가지고 있다.
- 평균값 = 중앙값 = 최빈값
- 1σ 안에 68.26%, 2σ 안에 95.44%, 3σ 안에 99.74%의 확률 변수 값이 포함된다.
- 정규 분포의 이런 조건은 단순한 수학적 성질에 그치지 않고, 실제 산업 현장에서도 중요한 기준으로 활용됩니다.
- 그 대표적인 예가 바로 '6-시그마'입니다. 품질 혁신을 뜻하는 6-시그마는 정규분포를 전제로, 평균에서 좌우로 ±6 표준편차 범위 안에 대부분의 제품이 들어오도록 변동을 최소화하는 전략입니다.
- 예시로 제품 100만 개당 3.4개 이하의 불량만 허용하겠다는 의미로, 사실상 무결점 수준의 품질을 목표로 합니다.
- 정규분포는 분포 간 비교를 위해 보통 표준화(Z-score) 후에 다루며, 이를 표준정규분포라고 합니다.
- 분포 평균과 분산에 따라 형태에 차이가 나게 되고, 다른 분포끼리 비교하고 면적을 계산하는 것은 복잡하고 어렵기 때문에 이런 표준화를 시켜야 하는 경우가 존재합니다.
지수 분포
- 지수분포는 특정 사건이 발생한 이후, 다음 사건이 발생하기까지 걸리는 시간을 모델링하는 데 사용되는 분포입니다.
- 즉, 데이터의 "모양"보다는 사건 간격의 패턴을 설명한다는 점에서 정규분포와는 다른 결을 가지고 있습니다.
- 평균에 따라 기울기가 정해지고, 앞선 포아송분포와 밀접하게 연관되어 있습니다.
- 예를 들어 A 가전업체의 A/S센터에 1시간당 평균 5회의 전화가 걸려온다면, 전화 간의 평균 시간 간격은 0.2시간이 됩니다.
- 즉, 포아송분포의 평균 λ은 5이며, 지수분포의 평균은 0.2가 되는 것입니다.
그럼 표본을 여러 번 뽑으면 어떤 분포가 나타나나요?
- "데이터의 분포는 제각각인데, 그렇다면 표본 평균의 분포는 어떤 모양을 가질까요?" 라는 질문이 생길 수 있습니다.
- 흥미롭게도, 데이터가 어떤 분포를 가지고 있든 간에 우리가 그 데이터를 여러 번 뽑아서 평균을 계산하면, 그 평균들의 분포는 점점 정규분포를 닮아갑니다.
- 바로 이 현상을 설명하는 이론이 중심극한정리(Central Limit Theorem)입니다.
- 이 이론은 표본의 양이 충분하면, 표본의 평균이 모집단의 평균과 유사해진다는 뜻이 아니고, 표본을 여러 번 추출했을 때, '각각의 표본' 평균들의 분포가 정규분포를 이룬다는 것입니다.
- 표본 크기가 특정 수준(일반적으로 30개 이상)을 초과하면 표본 평균의 분포는 중심 극한 정리로 인해 정규 분포에 가까워집니다.
- 그러나 모집단 분포가 심하게 치우쳐 있거나, 극단적인 경우에는 표본 평균의 정규 분포를 달성하기 위해 더 많은 표본이 필요할 수 있습니다.
- 아무튼 이 정리를 이용하면 모집단의 분포가 어떤 형태인지는 몰라도, 표본을 충분히 추출하면 표본 평균들의 분포가 정규분포를 이루기 때문에 통계적 추정이 가능해지게 됩니다.
- 예를 들어 만약 추출한 표본의 평균이 87이라면 모수의 실제 평균이 87±1σ일 확률은 68%라고 추정할 수 있는 것입니다.
참고 도서
- 『데이터 분석가가 반드시 알아야 할 모든 것』, 저자 황세웅, 위키북스
728x90
LIST
'데이터 분석 > 이론' 카테고리의 다른 글
| 데이터는 우연을 계산한다 (0) | 2025.10.21 |
|---|---|
| 평균은 시작일 뿐이다 (0) | 2025.10.20 |
| 데이터한테도 MBTI가 있다...? (0) | 2025.10.16 |
| 고양이 100마리로 서울의 모든 고양이 수를 알 수 있을까? 🐈 (0) | 2025.10.15 |
| 데이터를 다룬다면 통계학은 선택이 아니라 '기본'이다 (2) | 2025.10.14 |
