728x90
SMALL
- 평균은 데이터를 대표하는 값이긴 하지만, 평균만으로는 데이터의 모든 것을 다 파악할 수는 없습니다.
- 값들이 얼마나 흩어져 있는지, 한쪽으로 치우쳐 있는지, 그리고 얼마나 뾰족한 분포를 가지는지에 따라 데이터의 해석은 완전히 달라지게 됩니다.
- 그래서 통계학에서는 평균을 시작으로 분산, 표준편차, 왜도, 첨도 등의 기술 통계적인 특성을 함께 살펴봅니다.
평균은 데이터를 얼마나 잘 대표할까요?
- 우선 평균을 측정할 수 있는 방법은 상황의 특성에 따라 조금씩 다릅니다.
- 먼저 저희가 흔히 알고 있는 평균은 산술 평균인데, 기본적인 평균의 측정 방법입니다. 산술 평균은 등간 척도나 비율 척도로 측정된 데이터를 통해 전체 변숫값을 모두 더한 뒤에 값들의 개수로 나눠 구할 수 있습니다.
- 단순히 한 학급의 평균 몸무게나 키를 구하는 경우에는 이러한 산술 평균을 사용합니다.
- 그런데 각 학년의 몸무게 평균을 구할 때에는 학급마다 학생 수가 다르기에 각 학급의 관측치 수를 고려해줘야 합니다.
- 그래서 더 많은 비중을 차지하는 집단에 가중치를 더해 합리적인 평균값을 구해줘야 합니다. 소비자 물가 지수를 구할 때에도 이러한 가중 평균을 이용합니다.
- 그리고 일반적으로 시간에 따라 비율적으로 변하는 값의 평균을 구할 때(물가 상승률이나 인구 변동률, 증권의 수익률 등을 구할 때) 에는 기하 평균을 사용합니다.
- 마지막으로 이 기하 평균이 비율의 평균을 구하는 것이라면 조화 평균은 값의 평균을 구하는 것입니다.
- 대표적인 예시로 A 지점에서 B 지점으로 갈 때에는 80km/h, 돌아올 때는 120km/h로 왕복했을 경우의 평균 속도는 산술 평균으로는 100km/h인데, 같은 거리를 더 빠르게 갔을 때는 이동 시간이 줄어들기 때문에 산술 평균을 사용해서는 안 됩니다.
- 그래서 왕복한 전체 거리를 소요된 시간으로 나누는 조화 평균 계산 방법을 사용해야 합니다.

- 그런데 데이터에 극단적인 이상치가 포함되어 있을 경우에는 이런 평균 값들이 큰 영향을 받게 됩니다. 그리고 변숫값의 분포가 극단적으로 비대칭인 경우에도 평균으로 중심 성향을 파악하기 어렵습니다.
- 이러한 이유로 중앙값이나 최빈값이 평균값 대신 사용되기도 합니다.
- 그 중 중앙값은 데이터가 홀수 개라면 정가운데에 있는 값, 그리고 짝수 개면 중앙 부근 두 값의 산술 평균 값으로 정해집니다.
- 최빈값은 데이터 중 가장 빈도가 높은 값인데, 둘 이상이 존재할 수도, 없을 수도 있습니다. 최빈값은 평균이나 중앙값과 달리 명목 척도나 서열 척도로 이루어진 데이터도 측정이 가능합니다.
- 실무에서는 공장에서 생산하는 옷이나 신발 사이즈 비중을 설정할 때 활용될 수 있습니다.

평균과 항상 함께 등장하는 분산!은 언제 쓰나요?
- 보통 평균 편차(편차의 절댓값을 모두 더하고 관측치의 개수로 나눠주는 편차)가 분산보다는 더 직관적이긴 하지만, 컴퓨터를 이용해 계산하는 것이 굉장히 불편합니다.
- 그리고 평균 편차는 미분이 되지 않기 때문에 ML 모델에 필수적이라고 할 수 있는 손실 함수의 미분을 수행할 수 없습니다.
- 그렇다고 분산을 쓰자니 편차 제곱 값의 평균이기 때문에 관측치들이 얼만큼 떨어져 있는지를 바로 알기가 어렵습니다. 따라서 분산에 제곱근 값을 구해 실제 편차의 규모와 유사하게 조정한 것이 표준 편차입니다.
- 표본의 경우에는 관측치의 수로 바로 나눠주기보다는 자유도(관측치의 수-1)로 나눠주어야 합니다.
- 여기서 자유도는 자유롭게 선택할 수 있는 숫자의 개수를 의미하는데, 우선 표본은 당연하게도 모집단보다 분산이 작게 계산되는 경향이 있습니다.
- 왜냐 ! 모집단에서 뽑아다 쓴 것이니 당연히 그 범위는 줄어들 수 밖에 없는 법 !
- 그래서 이 표본의 분산이 작게 계산되는 것을 완화하기 위해 나눠주는 값을 -1 해줌으로써 모수의 분산과 비슷하도록 조정해주는 것입니다.

산포도를 측정할 수 있는 다른 방법도 있나요?
- 분산과 표준 편차 이외에도 범위, 사분위수, 변동 계수를 통해 산포도를 측정할 수 있습니다.
- 범위는 최솟값부터 최댓값까지를 의미하며, 최댓값에서 최솟값을 빼주면 구할 수 있습니다.
- 사분위수는 정규 분포를 따르지 않거나 산포도가 큰 경우에 자주 사용하는데, 데이터를 4등분한 각 지점을 의미합니다.
- 10분위수도 가끔 사용하는데, 이는 ML 모델 성능 측정할 때 활용됩니다.
- 변동 계수(CV)는 표준 편차를 산술 평균으로 나누어준 값입니다. 이 값으로 다른 두 자료의 산포도를 비교할 수 있습니다.
- 예를 들어 A 집단 30명의 발 사이즈와 키의 산포도를 비교하려고 한다면, 표준 편차만으로는 산포도를 비교할 수가 없습니다.
- 발 사이즈는 보통 평균에서 1cm, 많아봐야 3cm 정도씩 차이가 날테지만, 키는 10cm~15cm 정도의 범위씩 차이가 날 수도 있기 때문입니다.
- CV는 100을 곱해서 퍼센트로 나타내기도 합니다. 한편, 자료의 평균이 0이거나 0에 가까우면 CV가 무한히 커질 수도 있기 때문에 주의해야 합니다.
왜도와 첨도는 뭔가요?
- 왜도는 데이터 분포의 좌우 비대칭도를 표현하는 척도입니다. 즉, 얼마나 대칭이 아닌지를 나타내는 값입니다. 좌우 대칭을 이룰수록 왜도 값은 작아지고, 한쪽으로 몰려있게되면, 왜도 값이 증가합니다.
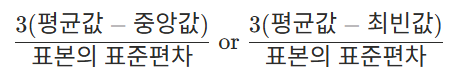
- 오른쪽 긴 꼬리의 분포를 띠는 경우는 양수를, 반대의 경우에는 음수를 가집니다. 그리고 보통 0보다 작거나 3보다 크면 데이터가 정규성을 가지지 않는다고 판단합니다.
- 뒤에서 나올 t-검정이나 ANOVA, 회귀 분석 등은 데이터가 정규성을 가진다는 전제를 깔고 있는데, 만약 정규성을 만족하지 않으면 데이터의 중심이나 변동성을 제대로 표현하지 못해, 비모수 검정 같은 방법을 사용합니다.
- 첨도는 분포가 정규 분포보다 얼마나 뾰족하거나 완만한지의 정도를 나타내는 척도입니다. 중심에 몰려 있을수록 뾰족해지고, 퍼지면 구름 모양을 띠게 됩니다.
- 첨도 값이 기준보다 크면 양의 첨도 혹은 급첨이라 하고, 작으면 음의 첨도 혹은 완첨이라고 합니다.
- 기본적으로는 3이 기준 값이지만, 해석의 편의상 -3을 해 0을 기준 값으로 하는 경우도 있습니다.

표준 편차는 분석에서 어떤 식으로 사용되나요?
- 데이터가 정규 분포로서 종 모양으로 좌우 대칭 형태일 때 이런 경험적 사실이 적용될 수 있습니다.
- 데이터의 약 68%는 평균으로부터 ±1 표준 편차 이내에 속합니다.
- 데이터의 약 95%는 평균으로부터 ±2 표준편차 이내에 속합니다.
- 데이터의 약 99.7%는 평균으로부터 ±3 표준편차 이내에 속합니다.
- 예를 들어 설탕 공장에서 500g짜리 봉지를 생산하는데, 표준 편차가 5g이라면, 500g과 505g 사이의 설탕 봉지는 전체의 약 34%에 이르게 되는 것입니다.
- 그리고 이로써 데이터의 범위도 표준 편차의 약 6배에 해당한다는 것도 알 수 있게 됩니다. 하지만 경험 법칙은 통계적으로 표본의 크기가 최소 100 이상은 되어야 성립합니다.
- 만약 주어진 데이터가 정규 분포가 아니거나 분포를 모를 경우에는 체비셰프의 정리를 적용할 수 있습니다.
- 해당 이론에 따르면 분포의 모양과 상관없이 평균값 ±2 표준편차 범위에 반드시 75% 이상의 데이터가 존재하고, ±3 범위에서는 적어도 89%, ±4 범위에서는 적어도 94%가 존재한다고 합니다.
참고 도서
- 『데이터 분석가가 반드시 알아야 할 모든 것』, 저자 황세웅, 위키북스
728x90
LIST
'데이터 분석 > 이론' 카테고리의 다른 글
| 데이터는 우연 속에서 패턴을 찾는다 (0) | 2025.12.03 |
|---|---|
| 데이터는 우연을 계산한다 (0) | 2025.10.21 |
| 데이터한테도 MBTI가 있다...? (0) | 2025.10.16 |
| 고양이 100마리로 서울의 모든 고양이 수를 알 수 있을까? 🐈 (0) | 2025.10.15 |
| 데이터를 다룬다면 통계학은 선택이 아니라 '기본'이다 (2) | 2025.10.14 |
