728x90
SMALL
- 오늘은 딥러닝에 대해 아주 간략한 내용을 배운 뒤에, 기초 ANN 관련 지식들을 습득해보았습니다.
🏃🏻 먼저 배운 내용으로 붓꽃 품종 분류하기!
- 어제 잠깐 언급되었던 붓꽃 품종을 분류하는 작업을 머신러닝으로 진행해보았습니다. (소프트맥스 회귀)
⚠️ Tensorflow Import할 때마다 요상한 메시지가...?
oneDNN custom operations are on. You may see slightly different numerical results due to floating-point round-off errors from different computation orders. To turn them off, set the environment variable TF_ENABLE_ONEDNN_OPTS=0.
- Spyder에서 작업하시는 분들은 Tensorflow를 Import할 때마다 위 메시지가 발생하는 것을 확인할 수 있습니다.
- 이 메시지는 TensorFlow를 import할 때 내부적으로 oneDNN(oneAPI Deep Neural Network Library)의 최적화가 활성화되어 있음을 알리는 정보성 로그입니다.
- 이에 따라서 부동소수점 연산의 순서가 달라질 수 있기 때문에, 같은 연산이라도 약간 다른 수치적 결과(소수점 이하 매우 작은 차이)가 발생할 가능성이 존재한다라는 뜻이고,
- TF_ENABLE_ONEDNN_OPTS=0으로 환경 변수를 설정하면 oneDNN 최적화를 비활성화할 수 있긴 한데...
- 메시지가 단순한 정보성 로그라서 동작에 영향을 주진 않기 때문에 무시하면 될 것 같습니다! 결론은 무시가 답!
✨ 데이터를 전처리하고 모델을 구축해보자!
- Iris 데이터셋에는 꽃잎길이, 꽃잎폭, 꽃받침길이, 꽃받침폭 그리고 품종 정보가 있습니다.
- 품종(클래스)은 문자열 형태이므로, pd.get_dummies를 사용해 원-핫 인코딩을 진행했습니다.
- 이렇게 하면 종속변수는 품종_setosa, 품종_versicolor, 품종_virginica의 세 개의 컬럼으로 구성되고, 독립변수는 네 개의 피처(꽃잎길이, 꽃잎폭, 꽃받침길이, 꽃받침폭)로 구성됩니다.
- 모델 구조는 입력 레이어(Input(shape=[4]))의 입력 데이터가 4차원임을 작성해주고,
- Dense(3, activation='softmax')를 통해서 4개의 입력을 받아 3개의 뉴런(클래스)을 출력하게 해줍니다.
- 그리고 출력층에서 softmax 함수를 사용해서 각 클래스에 대한 확률을 반환합니다.
✨ get_weights() 결과를 뜯어보자!
- model.get_weights()의 출력은 두 개의 배열(가중치, 편향)로 구성되어 있습니다.
💡 가중치 행렬 (Weights)
array([[ 0.7014372 , -0.23760743, -0.37519217],
[-0.3302868 , 0.2101829 , 0.2305736 ],
[-0.5867994 , -0.02816602, 0.45218867],
[-1.2004237 , 0.70238894, 0.48352575]], dtype=float32)- 크기(shape)는 (4, 3)으로 4개의 입력 피처와 3개의 출력 뉴런(클래스) 사이의 연결 가중치를 나타냅니다.
- 각 행은 하나의 입력 피처에 해당하며, 각 열은 해당 입력이 출력 뉴런에 미치는 영향을 나타냅니다.
- 결론적으로 첫 번째 뉴런(출력 클래스 1)에 대한 계산은 다음과 같이 이루어집니다.
$${\small \text{출력}_1 = (0.7014 \times \text{꽃잎길이}) + (-0.3303 \times \text{꽃잎폭}) + (-0.5868 \times \text{꽃받침길이}) + (-1.2004 \times \text{꽃받침폭}) + \text{bias}_1 }$$
💡 편향 행렬 (Bias)
array([ 0.20987847, 0.40736112, -0.56703424], dtype=float32)- 크기(shape)는(3,)으로 각 출력 뉴런에 대응하는 편향 값을 의미합니다.
- 각 뉴런에 추가되어 선형 변환 후 활성화 함수(softmax)에 들어가기 전, 출력값을 조정하는 용도로 사용됩니다.
✨ model.summary()도 뜯어보자!
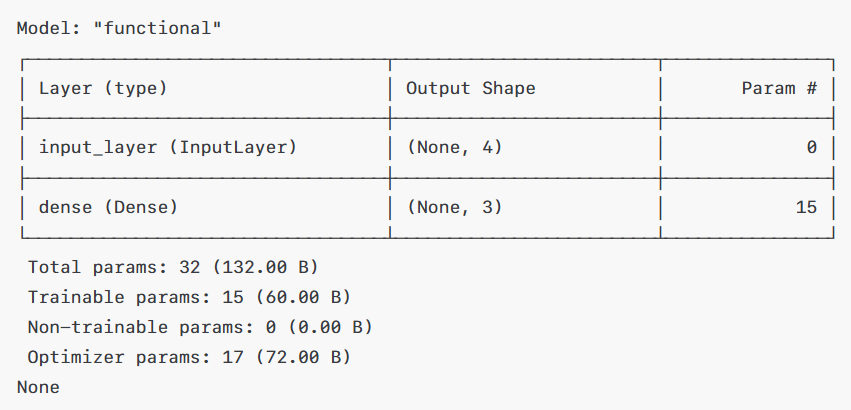
💡 레이어별 상세 정보
- InputLayer는 출력 형태가 (None, 4)인데, 여기서 None은 후에 배울 배치 크기이며, 각 샘플이 4개의 피처로 구성되었다는 것을 의미합니다.
- 파라미터는 0으로 입력 레이어는 학습 파라미터가 없다는 것을 의미합니다.
- Dense 레이어는 출력 형태가 (None, 3)이고, 각 입력 샘플에 대해 3개의 출력값(각 클래스의 확률)을 계산한다는 뜻입니다.
- 모델이 학습하는 파라미터 수는 총 15개이고 가중치가 4(입력 수) × 3(출력 수)로 12개, 편향이 3개로 총 15개가 되는 것입니다.
💡 전체 파라미터 수는?
- Trainable 파라미터는 Dense 레이어의 가중치와 편향으로, 총 15개이고,
- Optimizer params이 17개로 나와있는데, 옵티마이저(여기서는 아마도 기본 Adam이나 다른 옵티마이저를 사용했을 가능성이 있음)와 관련된 추가 내부 상태(모멘텀, 적응 학습률 등) 파라미터가 포함되어 있는 것 같습니다.
- 그래서 총 파라미터 수는 모델 파라미터(15개)와 옵티마이저 파라미터(17개)를 합한 32개가 나오게 됩니다.
🌊 이제는 딥러닝!
- 딥러닝은 머신러닝의 한 분야로, 뒤에 배울 인공 신경망(Artificial Neural Network)을 여러 층으로 깊게 쌓아 데이터를 학습하는 방식입니다.
- 인공 신경망을 기반으로 하고, 층이 깊어질수록 복잡하고 추상적인 패턴을 학습할 수 있습니다.
⏳ 퍼셉트론의 역사...와 구조
- 퍼셉트론은 1957년 프랭크 로젠블라트(Frank Rosenblatt)가 제안한 초기 인공 신경망입니다.
- "다수의 입력"으로부터 "하나의 결과"를 내보내는 간단한 알고리즘이라고 보시면 됩니다.
- 실제 뇌의 뉴런(신경 세포)에서 가지돌기가 여러 신호를 받아들여 축삭돌기를 통해 다음 뉴런에 전달하는 방식을 따온 알고리즘으로,
- 이 과정을 입력값($x$)과 가중치($w$), 그리고 출력값($y$)으로 모델링하게 된 것입니다.
💡 퍼셉트론은 어떻게 구성되어 있지?
- 여러 개의 입력 $x_1, x_2, \dots, x_n$ 각각에 가중치 $w_1, w_2, \dots, w_n$가 곱해져서 뉴런에 전달되는 형식으로,
- 입력과 가중치의 곱들을 모두 더한 값이 임계치(threshold)를 넘으면 1을, 넘지 못하면 0을 출력하는 구조입니다.
- 이때 출력 여부를 결정하는 활성화 함수가 계단 함수(Step Function)입니다.
- 이후에 발전된 신경망에서는 시그모이드 함수, 소프트맥스 함수 등 다양한 활성화 함수를 도입해서 성능과 표현력을 높이게 되었습니다.
- 퍼셉트론에는 추가로 편향이라는 상수 입력을 두어서, 뉴런의 출력이 더 유연하게 조절될 수 있도록 해줍니다.
✨ 단층 퍼셉트론과 논리 게이트
- 입력값을 받아들이는 입력층(Input Layer)과,
- 입력층으로부터 전달된 값을 바탕으로 최종 출력을 내는 출력층(Output Layer).
- 이 두 층만으로 구성된 퍼셉트론을 단층 퍼셉트론이라고 합니다.
- 단층 퍼셉트론은 직선(2차원) 혹은 평면(3차원 이상) 하나로 데이터를 두 영역으로만 분리할 수 있는 문제에 대해서만 해답을 찾을 수 있기 때문에
- 나중에 나올 복잡한 패턴(XOR 게이트 등) 분류에는 적합하지 않습니다.
💡 논리 게이트(Logic Gate)
- 컴퓨터에서 0과 1을 입력해서 새로운 값을 산출하는 회로를 게이트(gate)라고 합니다.
- 단층 퍼셉트론을 이용하면 특정 가중치와 편향 값을 설정해서, AND 게이트, NAND 게이트, OR 게이트를 구현할 수가 있습니다.
💡 AND 게이트
- 입력 $x_1, x_2$가 모두 1일 때만 출력 $y$가 1이 나오는 게이트입니다.
def AND_gate(x1, x2):
w1, w2 = 0.5, 0.5
b = -0.7
result = x1*w1 + x2*w2 + b
return 1 if result > 0 else 0
💡 NAND 게이트
- 입력 $x_1, x_2$가 모두 1일 때만 출력 $y$가 0이 나오는 게이트입니다.
def NAND_gate(x1, x2):
w1, w2 = -0.5, -0.5
b = 0.7
result = x1*w1 + x2*w2 + b
return 1 if result > 0 else 0- AND 게이트의 가중치와 편향에 부호만 바꿔도 NAND 게이트가 될 수 있습니다.
💡 OR 게이트
- 입력 $x_1, x_2$ 중 하나라도 1이면 출력 $y$가 1이 나오는 게이트입니다.
def OR_gate(x1, x2):
w1, w2 = 0.6, 0.6
b = -0.5
result = x1*w1 + x2*w2 + b
return 1 if result > 0 else 0
💡 단층 퍼셉트론으로 XOR 게이트를 구현할 수 없는 이유?!
- XOR 게이트는 입력값이 서로 다를 때(0,1 혹은 1,0)만 출력값이 1, 같으면 0이 출력되는 게이트입니다.
- 단층 퍼셉트론은 직선 하나로 데이터를 구분해야 하는데, XOR의 경우는 직선 하나로 0과 1을 완벽히 분리할 수 없기 때문에
- 결론적으로 단층 퍼셉트론은 XOR 게이트를 구현할 수 없고, 복잡한 분류 문제를 해결하기 위해서는 다층 퍼셉트론(Multi-Layer Perceptron)과 같은 더 깊은 구조가 필요하게 됩니다.
✨ 그렇다면 다층 퍼셉트론은?
- 단층 퍼셉트론이 입력층과 출력층만 존재하는 구조라면,
- 다층 퍼셉트론(MLP)은 입력층과 출력층 사이에 은닉층(Hidden Layer)을 하나 이상 추가하는 구조입니다.
💡 XOR 문제와 은닉층
- XOR 게이트는 AND, NAND, OR 게이트 조합으로 만들 수는 있지만, 단층 퍼셉트론으로는 구현이 불가능합니다.
- 그래서 단층 퍼셉트론에 은닉층을 추가하게 되면, 직선 하나로 분리 불가능한 문제도 해결할 수 있게 됩니다.
- 더 나아가서 은닉층 개수를 2개 이상으로 늘린 인공 신경망을 심층 신경망(Deep Neural Network, DNN)이라 부릅니다.
💡 은닉층의 역할은 무엇일까?
- 복잡한 문제를 풀기 위해 은닉층의 개수와 각 층의 뉴런 수를 늘릴 수 있는데,
- 아까도 말했듯 은닉층이 늘어날수록, 더 복잡하고 추상적인 패턴 학습이 가능해집니다.
- 심층 신경망은 MLP만을 의미하지 않고, 추후에 배울 은닉층이 2개 이상인 다양한 신경망 구조(CNN, RNN 등)를 포괄할 수 있습니다.
💡 그래서 딥러닝이란?
- 지금까지의 게이트 예시에서는 가중치와 편향을 직접 설정해줬어야 했는데,
- 사실 머신러닝에서는 가중치를 자동으로 학습하기 위해 손실 함수와 옵티마이저를 사용합니다.
- 그래서 앞서 배웠던 심층 신경망을 학습시키는 과정을 딥러닝(Deep Learning)이라 부르게 되는 것입니다.
🛰️ 인공 신경망에 관련된 용어들을 살펴보자!
- 피드 포워드 신경망(Feed-Forward Neural Network, FFNN)은 입력층에서 시작된 정보가 오직 한 방향(출력층 방향)으로만 전파되는 신경망을 의미합니다.
- 그래서 다층 퍼셉트론(MLP)은 대표적인 FFNN 구조이고,
- 추후에 나올 순환 신경망(Recurrent Neural Network, RNN)은 은닉층의 출력을 다시 은닉층의 입력으로 사용해서 순환 구조를 가지는 신경망입니다.
✨ Dense Layer가 도대체 뭐지?
- 앞선 실습에서부터 계속 Dense라는 용어가 나오는데, 이 밀집층(Dense layer)은 전결합층(Fully-connected layer, FC) 또는 완전연결층이라고도 불리며,
- 어떤 층의 모든 뉴런이 이전 층의 모든 뉴런과 연결된 층을 의미합니다.
- 다층 퍼셉트론의 은닉층과 출력층은 일반적으로 전결합층 구조를 가지고, 전에 Keras로 실습했을 때에도 전결합층을 구현할 때 Dense() 함수를 사용하기도 합니다.
✨ 계단 함수와 딥러닝의 학습 과정
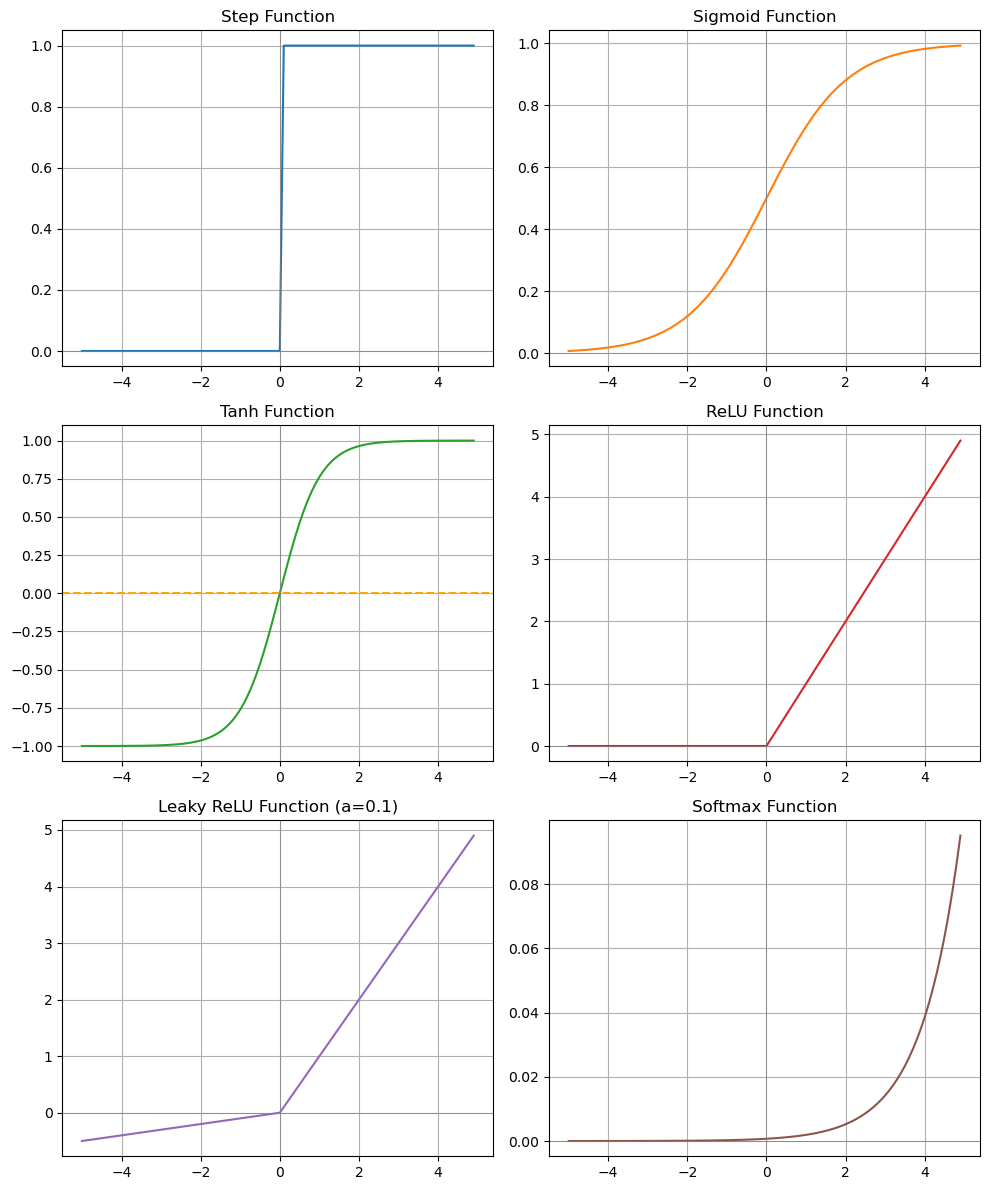
- 활성화 함수는 뉴런의 출력값을 결정해주는 함수를 의미하고 위와 같이 여러 활성화 함수가 존재합니다.
- 딥러닝의 활성화 함수는 선형함수가 아닌 비선형 함수를 사용해야, 은닉층을 쌓는 의미가 생기는데,
- 만약 모든 층에 선형함수만 사용하게 되면, 층을 아무리 늘려도 사실상 하나의 선형함수와 동일한 효과를 주기 때문입니다.
- 그 중에서도 활성화 함수를 사용하지 않는 선형층이 존재하긴 하는데,
- 예를 들어 임베딩 층(Embedding layer)의 경우에는 학습 가능한 가중치를 추가하는 의미는 있지만, 출력이 선형이기 때문에 비선형층과 구분지어 놓기는 합니다. 나중에 추가로 다뤄보겠습니다.
💡 계단 함수(Step Function)
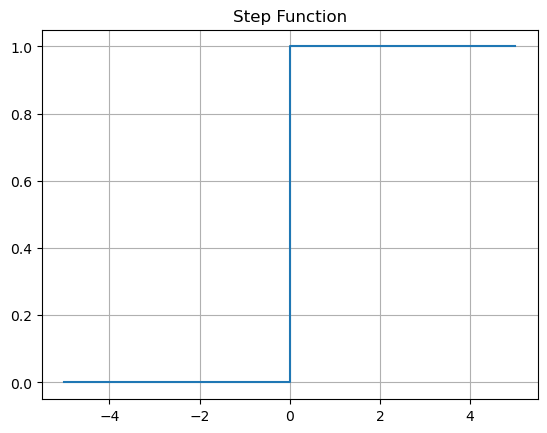
- 입력값이 0을 기준으로 양의 값이면 1을, 음의 값이면 0을 출력하는 함수입니다.
- 아까 퍼셉트론을 배울 때 잠깐 언급되었던 가장 기초적인 활성화 함수이지만,
- 최근에는 주로 다른 활성화 함수(시그모이드나 ReLU 등)를 사용하기 때문에 거의 쓰이지 않는 함수입니다.
💡 다른 것들을 보기 전에 인공 신경망이 어떻게 학습하는지 살펴보자
- 먼저 입력값이 뉴런들을 거쳐 출력층까지 전달되며 예측값이 계산되는 순전파(Forward Propagation)를 진행합니다.
- 그 후에 예측값과 실제값의 차이(오차)를 손실 함수로 계산하고,
- 손실값을 미분해서 각 가중치, 편향에 대한 기울기도 계산해줍니다.
- 마지막으로 경사 하강법 등을 활용해서 출력층에서 입력층 방향으로 기울기를 전달하며, 가중치와 편향을 업데이트시키는 역전파(Back Propagation)를 진행합니다.
✨ 시그모이드 함수(Sigmoid Function)
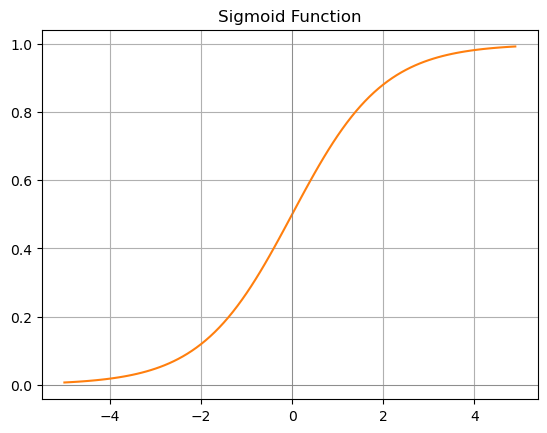
$$ \sigma(x) = \frac{1}{1 + e^{-x}} $$
- 출력 범위는 0에서 1 사이이고, 입력값이 큰 음수일 때 출력값이 0에 가깝고, 큰 양수일 때 1에 가까운 형태입니다.
- 출력값이 0 또는 1 근처일 때 기울기가 매우 작아지는데, 이 때문에 기울기 소실 문제가 발생합니다.
- 최대 미분값은 0.25로, 그 이상 커지지는 않는다고 합니다.
💡 기울기 소실(Vanishing Gradient) 문제
- 깊은 신경망에서 역전파 과정 중에 기울기가 0에 가까워져 앞쪽(입력층 방향)으로 전달되지 않는 현상을 의미합니다.
- 시그모이드 출력이 0 또는 1에 가까운 구간에서 미분값(기울기)이 극도로 작기 때문에 발생하고,
- 여러 은닉층을 지날수록 작은 값이 반복 곱셈되면서 점점 0에 가까워지게 되고,
- 결과적으로 앞단의 가중치가 업데이트되지 않아 학습이 불가한 상태가 됩니다.
💡 시그모이드 함수는 어디서 활용될까?
- 은닉층에서는 기울기 소실 문제를 유발하기 쉽기 때문에 시그모이드 함수를 지양해서 사용합니다.
- 대신 ReLU, Leaky ReLU, tanh 등 다른 활성화 함수가 주로 사용되는 편이고,
- 출력층에서만 출력값을 확률로 해석하는 데 유용하기 때문에 이진 분류 문제에서 많이 사용되는 편입니다.
✨ 하이퍼볼릭탄젠트 함수 (Hyperbolic tangent function, tanh)

$$ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$
- 출력 범위는 -1에서부터 1 사이의 범위를 가지며, 출력값이 0을 중심으로 분포해서 시그모이드 함수보다 기울기 소실 문제가 조금은 완화될 수 있었습니다.
- 하지만 여전히 입력값이 -1이나 1에 가까워지면, 기울기가 작아져서 깊은 신경망에서의 완벽한 해결책은 아니라고 봅니다.
- 미분값의 최댓값이 1로, 시그모이드 함수가 0.25인 것에 비해서는 상대적으로 큽니다.
- 그래서 장점이라고 하면, 시그모이드 함수 대비 0 중심으로 분포하고, 최대 미분값이 커서 학습 안정성이 더 좋긴 한데,
- 여전히 큰 음수나 큰 양수 영역에서 기울기가 작아져서 깊은 신경망에서는 여전하게도 기울기 소실 문제가 발생할 위험이 존재합니다. 다른 활성화 함수가 필요하겠네요.
✨ 렐루 함수(ReLU, Rectified Linear Unit)

$$ \text{ReLU}(x) = \max(0, x) $$
- 출력 범위는 $[0, \infty)$로 입력값이 음수이면 0을, 양수이면 그대로 출력하는 함수입니다.
- 시그모이드나 tanh와 다르게 출력값이 상한 없이 증가할 수 있기 때문에 큰 입력값에 대해서도 기울기가 1로 유지됩니다.
- 그리고 식만 봐도 알 수 있듯이 연산이 단순하기 때문에 계산량이 적고 학습 속도가 빠릅니다.
- 근데 음수 입력값이 들어오면 미분값(기울기)이 0이 되서 뉴런이 회생 불가능한 상태(죽은 렐루(dying ReLU) 문제)가 될 수도 있습니다. 그렇다면 또 다른 활성화 함수가 필요하겠네요...
✨ Leaky ReLU

$$ f(x) = \max(ax, x) \quad (a \text{는 매우 작은 양수}) $$
- ReLU 함수에서 dying ReLU 문제를 보완하기 위해 제안된 함수입니다.
- 음수 입력에 대해서도 0이 아닌 $a×x$를 반환해서, 기울기가 0이 되지 않도록 해줍니다.
- $a$는 하이퍼파라미터로, 음수 영역에서 기울기가 얼마나 새게(leak) 될지를 결정하는 변수입니다. (일반적으로는 0.01 등의 작은 값을 사용합니다.)
- ReLU와 계산량이 거의 비슷하고, 음수 영역에서도 학습 가능성을 유지할 수 있어서 좋은 함수입니다.
✨ 소프트맥스(Softmax) 함수

$$ \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}} $$
- 다중 클래스 분류 문제에서 출력층에 주로 사용되는 함수입니다. 이미 전에도 여러 번 써봤습니다!
- 시그모이드가 이진 분류(두 가지 클래스) 확률을 출력하는 반면, 소프트맥스는 여러 클래스에 대한 확률 분포를 출력합니다.
- 예를 들어서 총 5개 클래스라면, 각 클래스가 정답일 확률을 모두 합쳐서 1이 되도록 만들어주는 역할을 합니다.
- 출력층의 각 뉴런에서 나온 실수 값($z$)을 지수화해서, 전체 합으로 나누어 확률로 변환해주고,
- 가장 큰 지수값(가장 큰 $z$)을 갖는 뉴런이 가장 높은 확률을 가지게 되는 구조로 동작합니다.
🙅🏻♂️ 행렬곱으로 신경망 이해해보기
- 딥러닝 모델을 설계할 때 순전파의 과정을 행렬곱 연산으로 이해하면, 모델의 작동 원리와 매개변수의 수를 쉽게 파악할 수 있습니다.
- 여기서는 model.summary()는 위에서 다 뿌셔놨으니(?) 다층 퍼셉트론(MLP)만 간단하게 정리해보겠습니다.
✨ 순전파는 뭘까?
- 순전파는 입력 데이터가 입력층에서 시작하여 은닉층을 거쳐 출력층까지 전달되면서 예측값을 계산하는 과정입니다.
- 이때 각 층에서는 가중치와 편향이 적용되고, 최종적으로 활성화 함수를 거쳐 예측값을 출력합니다.
💡 다층 퍼셉트론에서의 순전파
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
# 1) 첫 번째 층: 입력 4개 → 은닉층1: 8개 뉴런, 활성화: ReLU
model.add(Dense(8, input_dim=4, activation='relu'))
# 2) 두 번째 층: 은닉층1: 8개 → 은닉층2: 8개 뉴런, 활성화: ReLU
model.add(Dense(8, activation='relu'))
# 3) 출력층: 은닉층2: 8개 → 출력: 3개 뉴런, 활성화: Softmax
model.add(Dense(3, activation='softmax'))- 배치 크기 1(단일 샘플) 기준으로 층별로 행렬의 크기를 추정해보면 다음과 같습니다.
- 입력층에서 은닉층1로의 행렬 크기는
$$ \mathbf{Y}_1 = \mathbf{X}\mathbf{W}_1 + \mathbf{b}_1 $$
- 은닉층1에서 은닉층2로의 행렬 크기는
$$ \mathbf{Y}_2 = \mathbf{Y}_1\mathbf{W}_2 + \mathbf{b}_2 $$
- 마지막으로 은닉층2에서 출력층으로의 행렬 크기는 아래와 같이 계산됩니다.
$$ \mathbf{Y}_3 = \mathbf{Y}_2\mathbf{W}_3 + \mathbf{b}_3 $$
- 참고로 활성화 함수(ReLU, Softmax 등)는 행렬의 크기를 변경하지 않고, 각 원소별로 적용됩니다.
🎒 딥러닝은 어떻게 학습될까?
✨ 손실 함수에 대해서
- 손실 함수는 실제값과 예측값의 차이를 수치화한 함수로, 딥러닝 모델이 학습할 때 최소화해야 하는 대상입니다.
- 문제 유형(회귀/분류)에 따라서 자주 사용하는 손실 함수들이 정해져 있습니다.
- 지금 설명하는 것들 이외에도 더 다양한 손실 함수가 있으며, Tensorflow 공식 문서(tf.keras.losses)에서 확인할 수 있습니다.
💡 MSE(Mean Squared Error)
- 회귀(연속형 값 예측)에서 주로 사용되고 코드로는
- loss='mse' 또는 loss=tf.keras.losses.MeanSquaredError()와 같이 사용됩니다.
💡 Binary Cross-Entropy
- 이진 분류(출력층에 시그모이드)에서 사용되는 손실 함수로 코드로는
- loss='binary_crossentropy' 또는 loss=tf.keras.losses.BinaryCrossentropy()와 같이 사용됩니다.
💡 Categorical Cross-Entropy
- 다중 클래스 분류(출력층에 소프트맥스)에서 사용되고, 코드는
- loss='categorical_crossentropy' 또는 loss=tf.keras.losses.CategoricalCrossentropy()처럼 사용됩니다.
💡 Sparse Categorical Cross-Entropy
- 원-핫 인코딩 없이 정수 레이블로 학습할 때 사용되는 손실 함수로,
- loss='sparse_categorical_crossentropy'로 사용할 수 있습니다.
✨ 배치 크기(Batch Size)에 따른 경사 하강법에 대해서
- 딥러닝에서는 손실 함수를 줄이기 위해 경사 하강법을 사용합니다.
- 이때 배치(Batch)라는 개념이 중요한데, 한 번의 매개변수 업데이트에 사용되는 데이터 개수를 배치 크기라고 부릅니다.
- 이 경사 하강법에도 여러 가지 종류가 있습니다.
💡 배치 경사 하강법 (Batch Gradient Descent)
- 전체 데이터로 손실을 계산한 다음, 매개변수를 한 번 업데이트하는 경사 하강법입니다.
- 전체 데이터가 큰 경우, 연산 비용과 메모리 요구량이 엄청나게 크기 때문에 주의해야합니다.
- model.fit(X_train, y_train, batch_size=len(X_train))처럼 사용할 수 있고, 코드에서 batch_size를 X_train 크기 전체로 잡은 것을 확인하실 수 있습니다.
💡 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
- 배치 크기를 1로 설정해서 매번 단 하나의 샘플에 대해 손실을 계산하고 매개변수를 업데이트하는 방식입니다.
- 업데이트 속도는 빠르지만, 손실이 불안정하게 변동할 수 있습니다.
- model.fit(X_train, y_train, batch_size=1)처럼 batch_size는 1로 설정하게 됩니다.
💡 미니 배치 경사 하강법 (Mini-Batch Gradient Descent)
- 배치 크기를 1과 전체 데이터 사이의 적당한 값(32, 64, 128 등)으로 설정하는 방법입니다.
- 전체 데이터로 하는 것보다 빠르고, 배치 크기가 1인 SGD보다 상대적으로 안정적이라고 할 수 있습니다.
- 실제 딥러닝에서 가장 많이 사용되는 방법으로 model.fit(X_train, y_train, batch_size=128)와 같이 적당한 값을 주어 사용할 수 있습니다.
✨ 옵티마이저(Optimizer)에 대해서
- 경사 하강법을 기반으로 하되, 학습률이나 관성(momentum) 등을 조정해서 성능을 개선한 다양한 알고리즘도 있습니다.
💡 Momentum
- 관성을 적용해서 로컬 미니멈을 탈출하는 데 도움을 주는 역할을 합니다.
- 예를 들어 keras에서 tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)와 같이 모멘텀을 인자값으로 넘겨줄 수 있습니다.
💡 Adagrad
- 매개변수마다 다른 학습률을 적용하는 기법입니다.
- 많이 변동하는 파라미터에는 학습률을 낮게, 적게 변동하는 파라미터에는 학습률을 높게 주는 방식입니다.
- tf.keras.optimizers.Adagrad(learning_rate=0.01, epsilon=1e-6)와 같이 사용할 수 있습니다.
💡 RMSprop
- Adagrad가 학습을 계속 진행한 경우, 나중에는 학습률이 지나치게 떨어진다는 단점이 있는데, 이 Adagrad를 다른 수식으로 대체하여 단점을 개선할 수 있었습니다.
- tf.keras.optimizers.RMSprop(learning_rate=0.001, rho=0.9, epsilon=1e-6)처럼 사용하시면 됩니다.
💡 Adam
- momentum과 RMSprop을 절충한 알고리즘입니다.
- tf.keras.optimizers.Adam(learning_rate=0.001, beta_1=0.9, beta_2=0.999)와 같이 사용합니다.
- 옵티마이저를 사용할 때, model.compile(optimizer=adam) 처럼 직접 인스턴스를 전달하거나, 'adam', 'sgd', 'rmsprop' 등 문자열로 지정해도 동작합니다.
✨ 에포크와 배치 크기, 이터레이션까지 알아보자!
- 에포크(Epoch)는 전체 데이터를 한 번 모두 학습(순전파+역전파)한 상태를 의미합니다.
- 예를 들어, 에포크를 50으로 준다는 뜻은 전체 데이터로 학습을 50번 반복한다는 뜻입니다.
- 배치 크기(Batch Size)는 매개변수를 업데이트할 때 사용하는 데이터 개수를 의미합니다.
- 예를 들면, 전체 데이터가 2000개이고, 배치 크기가 200으로 잡혀있다면, 한 번의 매개변수 업데이트 시 200개의 샘플을 사용하는 것을 뜻합니다.
- 이터레이션(Iteration)은 스탭(Step)이라고도 하는데, 한 에포크 내에서 매개변수를 업데이트하는 횟수를 의미합니다.
- 위의 예를 이어서 들게 되면, 전체 데이터 2000개, 배치 크기 200으로 준다면, 이터레이션은 2000 / 200 = 10회
- 즉, 에포크 1회당 매개변수 업데이트가 10번 일어나게 된다는 뜻입니다.
🤔 32일차 회고
- 어제 머신러닝을 와다다 끝내고, 이어서 오늘은 딥러닝을 쭉 달려보았습니다.
- 어제 배웠던 활성화 함수, 손실 함수도 전부 배워보았는데, 확실히 알고 듣는 것과 모르고 듣는 것의 차이는 큰 듯 합니다.
- 모르면 더 알고 싶고, 알면 더욱 알아가고 싶은 게 사람 마음인 것 같습니다.
- 이제 슬슬 프로젝트가 다가오고 있는데, 모르는 분야의 주제인 만큼 더욱 알기를 노력해서 저만의 정갈한 포트폴리오가 되어주었으면 좋겠습니다.
- 내일은 1차 프로젝트 기획서를 작성해야하는 날입니다. 수많은 데이터를 탐색하고 정리하는 시간을 가질텐데 또 계획대로 척척 진행되길 바라는 마음으로 다음 주를 맞이해보겠습니다!
728x90
LIST
'부트캠프 > LG U+' 카테고리의 다른 글
| 🤔 RNN과 LSTM 그리고 BiLSTM (6) | 2025.03.18 |
|---|---|
| 🤔 형태가 바뀌면 의미도 바뀔까? (0) | 2025.03.17 |
| 🤔 왜 달려도 달려도 끝이 없을까... (8) | 2025.03.12 |
| 🤔 Words In My Bag (8) | 2025.03.11 |
| 🤔 자연어를 전처리해보자 (7) | 2025.03.07 |

