728x90
SMALL
배낭 문제(Knapsack Problem)의 개념
- 배낭 문제란, 제한된 용량을 가진 배낭에 최대 가치를 담을 수 있는 물건들의 조합을 찾는 문제입니다. 각각의 물건은 가치와 부피(또는 무게)를 가지고 있으며, 우리의 목표는 주어진 용량 내에서 최대 가치를 얻을 수 있는 조합을 찾는 것입니다.
- 0/1 배낭 문제: 가장 기본적인 형태인 0/1 배낭 문제에서는 각각의 물건은 단 하나씩만 선택할 수 있습니다. 즉, 해당 물건을 전부 넣거나 아예 넣지 않거나 둘 중 하나만 선택할 수 있습니다.
코딩 테스트에서의 배낭 문제 접근 방법
- 일반적으로 0/1 배낭 문제를 해결하기 위해서 아래 일련의 단계를 거치는 다이나믹 프로그래밍(DP) 기법을 사용합니다.
- DP 테이블 초기화: DP 테이블은 (물건 개수+1) x (배낭 용량+1) 크기로 초기화합니다.
- 점화식 세우기: 각각의 물건에 대해 "넣었을 때와 넣지 않았을 때"의 경우를 고려하여 점화식을 세웁니다.
- DP 테이블 갱신: 점화식에 따라 DP 테이블 값을 계산하고 저장합니다.
- 최종 결과 도출: DP 테이블 마지막 값이 최대 가치가 됩니다.
- 다음은 0/1 배낭 문제를 해결하는 예시 코드입니다.
def knapsack(weights, values, capacity):
n = len(weights)
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, capacity + 1):
if weights[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], values[i - 1] + dp[i - 1][j - weights[i - 1]])
return dp[n][capacity]
weights = [2,3,4,5]
values = [3,4,5,6]
capacity = 8
max_value = knapsack(weights, values, capacity)
print(max_value)- 위 코드에서 weights 리스트와 values 리스트는 각각 물건들의 부피(무게)와 가치를 나타내며 capacity 변수는 배낭의 용량입니다. 함수 knapsack()은 최대 가치를 반환합니다.
1535번: 안녕
첫째 줄에 사람의 수 N(≤ 20)이 들어온다. 둘째 줄에는 각각의 사람에게 인사를 할 때, 잃는 체력이 1번 사람부터 순서대로 들어오고, 셋째 줄에는 각각의 사람에게 인사를 할 때, 얻는 기쁨이 1번
www.acmicpc.net
문제
- 세준이는 성형수술을 한 후에 병원에 너무 오래 입원해 있었다. 이제 세준이가 병원에 입원한 동안 자기를 생각해준 사람들에게 감사하다고 말할 차례이다.
- 세준이를 생각해준 사람은 총 N명이 있다. 사람의 번호는 1번부터 N번까지 있다. 세준이가 i번 사람에게 인사를 하면 L[i]만큼의 체력을 잃고, J[i]만큼의 기쁨을 얻는다. 세준이는 각각의 사람에게 최대 1번만 말할 수 있다.
- 세준이의 목표는 주어진 체력내에서 최대한의 기쁨을 느끼는 것이다. 세준이의 체력은 100이고, 기쁨은 0이다. 만약 세준이의 체력이 0이나 음수가 되면, 죽어서 아무런 기쁨을 못 느낀 것이 된다. 세준이가 얻을 수 있는 최대 기쁨을 출력하는 프로그램을 작성하시오.
해결 방법
- 이 문제에서는 체력을 소모하여 행복을 얻어야 합니다. 최대한 많은 행복을 얻어야 하며, 체력이 바닥나면 모든 것이 끝나기 때문에 주의해야 합니다. 이런 종류의 문제에서는 일반적으로 동적 계획법(Dynamic Programming)을 사용합니다.
import sys; input=sys.stdin.readline
N = int(input())
L = [0] + list(map(int, input().split()))
J = [0] + list(map(int, input().split()))
dp = [[0] * 100 for _ in range(N+1)]
for i in range(1, N+1):
for j in range(100):
if L[i] > j:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-L[i]] + J[i])
print(dp[N][99])- 위 코드에서 L 리스트와 J 리스트는 각각 체력 소모량과 얻을 수 있는 행복값을 나타내며, dp 배열은 해당 체력까지 사용했을 때 얻을 수 있는 최대 행복값입니다.
2629번: 양팔저울
첫째 줄에는 추의 개수가 자연수로 주어진다. 추의 개수는 30 이하이다. 둘째 줄에는 추의 무게들이 자연수로 가벼운 것부터 차례로 주어진다. 같은 무게의 추가 여러 개 있을 수도 있다. 추의 무
www.acmicpc.net
문제
- 양팔 저울과 몇 개의 추가 주어졌을 때, 이를 이용하여 입력으로 주어진 구슬의 무게를 확인할 수 있는지를 결정하려고 한다.
- 무게가 각각 1g과 4g인 두 개의 추가 있을 경우, 주어진 구슬과 1g 추 하나를 양팔 저울의 양쪽에 각각 올려놓아 수평을 이루면 구슬의 무게는 1g이다. 또 다른 구슬이 4g인지를 확인하려면 1g 추 대신 4g 추를 올려놓으면 된다.
- 구슬이 3g인 경우 아래 <그림 1>과 같이 구슬과 추를 올려놓으면 양팔 저울이 수평을 이루게 된다. 따라서 각각 1g과 4g인 추가 하나씩 있을 경우 주어진 구슬이 3g인지도 확인해 볼 수 있다.
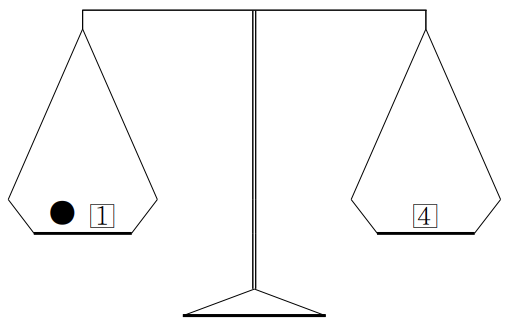
- <그림 2>와 같은 방법을 사용하면 구슬이 5g인지도 확인할 수 있다. 구슬이 2g이면 주어진 추를 가지고는 확인할 수 없다.
- 추들의 무게와 확인할 구슬들의 무게가 입력되었을 때, 주어진 추만을 사용하여 구슬의 무게를 확인 할 수 있는지를 결정하는 프로그램을 작성하시오.
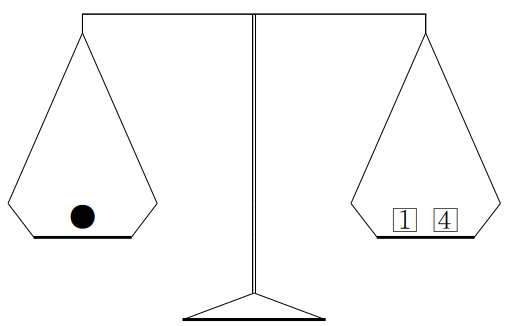
해결 방법
- 이 문제에서는 여러 개의 추가 있고, 그 추를 사용해서 원하는 무게를 만들 수 있는지 판별해야 합니다. 배낭 문제와 비슷하게 추를 선택하거나 선택하지 않거나를 고려하여 동적 계획법으로 해결할 수 있습니다.
import sys; input=sys.stdin.readline
N = int(input())
weights = list(map(int, input().split()))
M = int(input())
balls = list(map(int, input().split()))
possible = [False] * 40001
possible[0] = True
for weight in weights:
temp = [i for i, v in enumerate(possible) if v]
for t in temp:
possible[t + weight] = True
possible[abs(t - weight)] = True
for ball in balls:
if possible[ball]: print('Y', end=' ')
else: print('N', end=' ')- 위 코드에서 weights 리스트는 각 추의 무게를 나타내고, balls 리스트는 확인해야 하는 공의 무게를 나타냅니다. possible 배열은 해당 인덱스의 무게를 만들 수 있는지 여부를 저장합니다.
- 배낭 문제와 관련해서 심화적으로 분수적 배젤문자(일정 비율로 분할하여 담을 수 있는 경우도 고려하는 유형), 바운디드 베타문자(Bounded Knapsack)와 같은 주제들도 공부해보시면 도움이 될 것입니다.
728x90
LIST
'알고리즘 이론 > 코딩테스트 알고리즘' 카테고리의 다른 글
| 알면 도움되는 코딩 테스트 유형: 15) #Topological_Sorting (1) | 2023.09.15 |
|---|---|
| 알면 도움되는 코딩 테스트 유형: 14) #MST (1) | 2023.09.14 |
| 알면 도움되는 코딩 테스트 유형: 12) #Primality_Test (3) | 2023.09.12 |
| 알면 도움되는 코딩 테스트 유형: 11) #Two_Pointer (0) | 2023.09.10 |
| 알면 도움되는 코딩 테스트 유형: 10) #Priority_Queue (0) | 2023.09.08 |
