728x90
SMALL
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
def hanoi(n, start, target, aux, answer):
if n == 1:
answer.append([start, target])
else:
hanoi(n-1, start, aux, target, answer)
answer.append([start, target])
hanoi(n-1, aux, target, start, answer)
def solution(n):
answer = []
hanoi(n, 1, 3, 2, answer)
return answer왜 이렇게 풀었을까?
- 하노이의 탑은 재귀 문제 중에서도 팩토리얼 다음으로 유명하다고 볼 수 있는 문제입니다.
- 문제에 나와있는 1번, 2번, 3번 기둥을 코드에서는 각각 start, aux, target 기둥으로 표현했습니다.
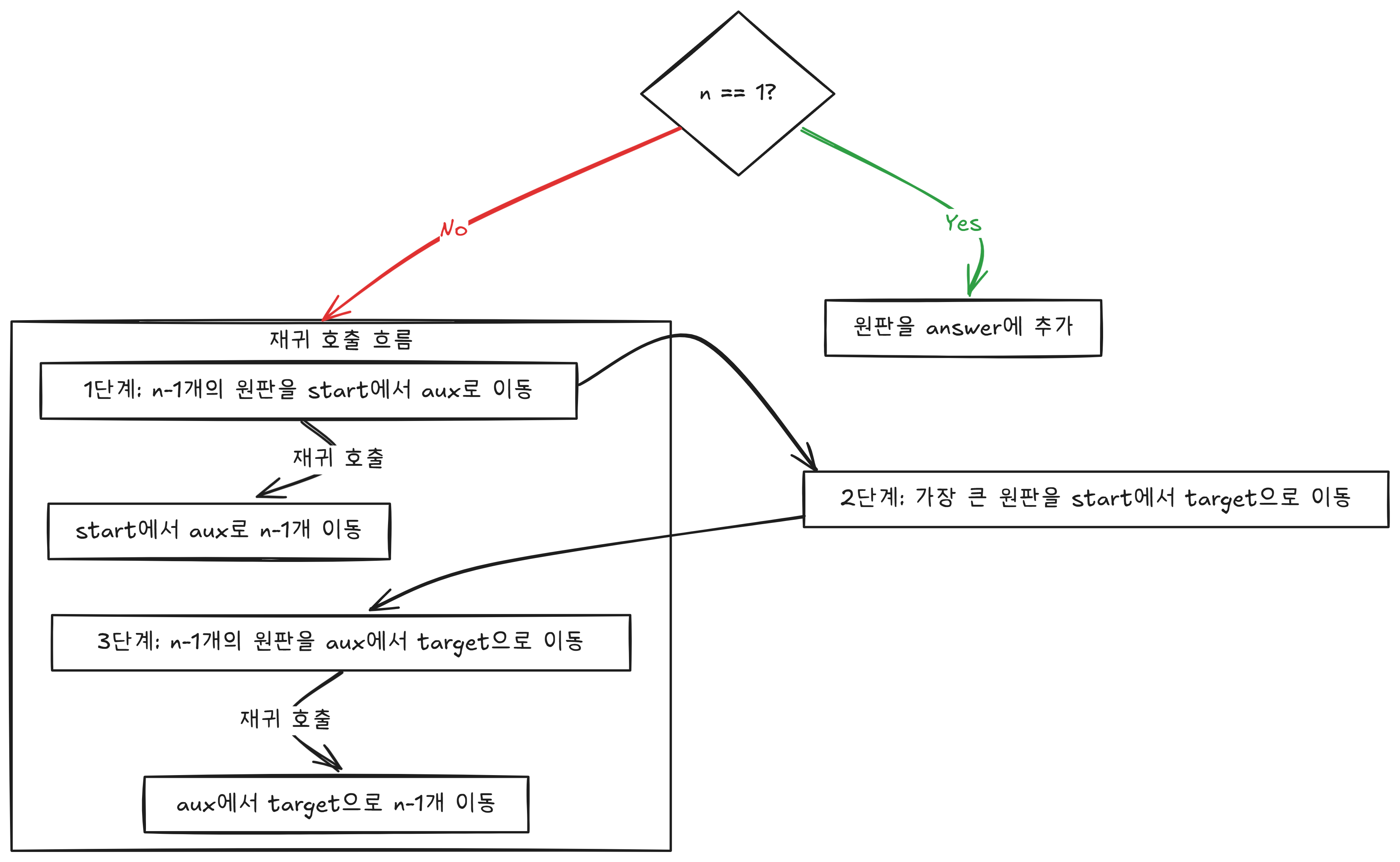
- 하노이의 탑은 크게 3가지 과정으로 나뉘어지는데,
- n-1개의 원판을 start에서 aux로 이동하는 과정 (재귀)
- 가장 큰 원판을 start에서 target으로 이동하는 과정 (O(1)의 시간 복잡도)
- aux에 있는 n-1개의 원판을 target으로 옮기는 과정 (재귀)
- 위 과정을 코드로 구현하면 결국 O(1)의 시간 복잡도를 가지는 부분에서 재귀가 종료되기 때문에
- answer에 해당 경로를 집어넣는(append) 과정을 반복하다보면 최종적으로 원판을 옮기는 모든 경로가 담기게 됩니다.
728x90
LIST
'알고리즘 문제 풀이 > 프로그래머스 (Level 2)' 카테고리의 다른 글
| 📗 우박수열 정적분 (6) | 2024.11.27 |
|---|---|
| 📗 멀쩡한 사각형 (1) | 2024.11.17 |
| 📗 가장 큰 정사각형 찾기 (2) | 2024.10.11 |
| 📗 거리두기 확인하기 (4) | 2024.10.07 |
| 📗 리코쳇 로봇 (0) | 2024.10.02 |
